Font size

System Formulation

Make and test (component) models

Introduction
The models developed through the implementation of the SAF will most probably not have many direct analogies in the literature. It would be rather useful for you to explore the published documents of the SPICOSA project as they provide a range of implementations, highlighting problems you will most probably face too and sometimes providing solutions or interesting ideas. In any case during your implementation your team of experts will have the responsibility to decide how to best represent your Virtual System in the simulation software. This is a procedure that requires time and good communication between your team. It is important to keep in mind that SAF is about communication: science & policy communication, but also about communication amongst the different science disciplines. While we demonstrate the development of separate components, this doesn’t mean that each component should be developed independently of the others. There must be a co-evolution: each component represents a part of the Virtual System so the scientific team should discuss the scope of the development in a sharing way. In the end the modeller is the one that will realize those common ideas in the simulation software, but the rest of the team should also have a part in the development by criticizing the functionality and ensuring, each from the point of view of his discipline, the correct behaviour of the model.

 Typical Virtual System models are hierarchical, and must be developed on several levels. The top level is the model of the cause-&-effect chain, made up of linked or separate ecological, economic and social sub-models. The second level is that of functional units - such as phytoplankton, or mussel farming cash flows - each containing system state variables linked by process equations. The third level is that of the process equations, containing local constants parameters for which values must be supplied.

It is also likely that your model or models will evolve with, and improve over, time, sometimes by means of an interative process in which an assmebly made at say an ESE component level is stripped back to funcitonal components and rebuilt. The table below sets out the terms we use for model complexity levels and developmental stages.

 

Table 1 : List of the model categories and levels.

Describing the model at process and functional levels.

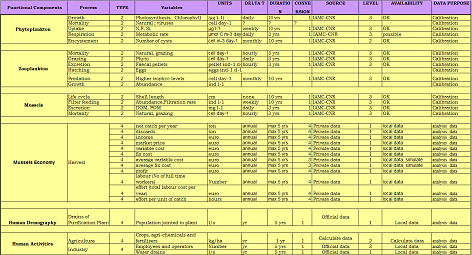
Table of Processes
This table will facilitate you in consolidating the information you will need later for the documentation of your model. Its purpose is to characterize and determine the key processes that are going to be used in your simulation models. Examples with tentative format are given to the following tables and also to some of the implementation examples accompanying this subtask. In any case the format is usually a matter of preference. Use one of those provided of create your own, making sure it incorporates all the important and necessary information.

Table a: This table contains the characteristics of the used processes, which are grouped according to their internal function in the Virtual System. Click on thumbnail for full version.

b. This table illustrates how you might document the process blocks or program sub-functions. Click on thumbnail for full version.

Level of Relevance
You should rank the key processes by using three major levels of relevance. This will help you during the model’s formulation in order to keep focused on the most important processes.

Highest Relevance (1):. Those processes that are essential to the cause-&-effect and/or to the impact-response chains. Relevant (2): These processes are required because they capture the nonlinear responses (e.g. feedback loops), control thresholds (i.e. change dynamics), or are necessary for a particular output (e.g. related to a scenario). Least Relevant (3): These are desirable to add extra stability (e.g. to dampen an instability), to calculate additional indicators, or to add to the quality of presentation or to the output.

Process Inputs & Outputs
In general, each process has an input and an output, which corresponds to the direction indicated by the order of the cause-&-effect or impact-response chains and determines the mass, energy, and information propagation. As such, the input to a process represents its interaction with the preceding process, and its output represents its interaction with the succeeding process.

Finding the data to test these may not always be simple. More specifically:

Inputs:
• You can compare the modelled process with a published set of data if available.
• You can acquire data for the input from your institute.
• You can simulate a data set for the input taking care to keep similar statistics.

Outputs:
It is necessary to check them for mathematical errors (validation) and to run rough comparisons with known data (preliminary calibrations).

Parameters and Constants:
Many processes require additional inputs, other than its primary variables. These may be constants or parameters calculated elsewhere. These need to be listed with the process.

Dimensions & Verification
A process converts the characteristics of the input into those of the output. This conversion often involves changes in dimensions. It is importance that you balance the dimensions of the formulation and the used units must be compatible.

Dimensional Analysis:
Dimensional analysis is a useful tool for model formulation. More specifically:
• to ensure you have a dimensionally compatible set of variables in your formulation.
• to handle dependencies between variables and express them as a formula.

Verification:
You will have to conduct a more complete validation on the refined process models, later during formulation. At this stage it is important to verify that the mathematical expressions you are using are correct, and note the reference wherever appropriate.

Process Function
You should include a comprehensive summary in the Process Table concerning the role of each and every process in the simulation. If a feedback loop, threshold, or potential instability is included you should provide the appropriate explanations.

Degree of Approximation
The main suggestion is that you use three degrees of approximation for the formulation of processes. The reason for this is that:

• the accuracy of a simulation model is limited by the link that is least well formulated. You do not want to spend resources on perfecting one process and leave another with only a primitive approximation.

• it is not always necessary to improve a formulation. Only after you have developed a rough model you are able to quantify the sensitivity of the formulation to the internal parameters or to the Inputs. It is possible that you realise that your solution is not presenting important variations to an Input for which you have difficulty acquiring better data and therefore improvement may not be necessary.

• the approximations you will make should not always be the easiest or most simple available. They need to reflect the level of relevance to your Policy Issue, in the sense that the most important processes might require a higher degree of approximation.

You should choose the degrees of approximation analogous to the categories of models (Table1).

Ballpark:
This is the simplest approximation possible during the formulation. It is simple because it uses only the most fundamental variables and parameters, and for these it uses simplified approximations, e.g. linear dependencies, analogue fits of empirical data, etc. More specifically:

• the amount of light available for phytoplanktonic growth can be simply taken as fraction of the light at the surface of the estuary.

• the amount of the rainwater arriving to the river or the estuary by the surface flow can be simply taken as a fraction of the recorded rainfall.

• the increased sewage load caused by tourists could be approximated through multiplying the number of tourists by the statistical average loading/per person.

Refined:
The refined degree of approximation is a best guess of what is necessary to represent the functionality of the process in the expected context of the simulation. More specifically:

• you know that in your shallow estuary you need to calculate the light at the bottom and that it will vary with the amount of algae in the water column. You then add a light adsorption coefficient that is a function of the algae concentration. You may then test some approximations of this added dependency.

• you know that the ballpark approximation may be adequate when dealing with mean values of runoff, but you need to capture the response to rain events. You then add an infiltration process that depends on the rate of rainfall, the moisture content of the soil, the evaporation rates, land inclination, etc. as appropriate to your case.

• you know that among the tourists, there is a significant variability in diet that relates to the Nitrogen loading. You simulate this by fractionating the tourists’ population by country of origin and multiply by the statistics of their country, or you could survey the frequency distribution among local restaurants.

Final:
The final degree of approximations is the one used in the simulation model. In this form, it represents the best possible development and it is ready for scientific and other publication with the appropriate justifications. The final model will be ready in the Appraisal Step.

Make and test functional units

Formulation of Processes
After defining the equations that you will use for the description of processes, it is rather easy to proceed to the formulation, in a ballpark level. For the processes that you have available data you must make initial validation checks. If data are not available, since you are still in a ballpark level, means and standard deviations deriving from literature can accommodate you in checking the validity of your formulation.

Functional Units
The Functional grouping of processes is somewhat arbitrary and it depends a lot in your judgement and understanding of the Virtual System’s functionality. This draft grouping should be reflected to your Process Table (see example a). From now on we will refer to these groups as “functional units” of the Virtual System. Your main objective should be to group inter-related processes in such a way that the inputs and outputs of the group are significantly less than the number of processes internal to the group. This will facilitate you during the calibration process and will also present organizational advantages during the modelling process.

At this stage you should complete all the ballpark representations of the functional units before making further improvements. This means you will need to stop and evaluate how well these have captured the functionality that you need for the simulation model. From this evaluation, you will proceed to the processes refinements in the next subtask.

Checking Performance
You should check all the functional units by following the procedure that was used for checking the process formulations. That means that you must run them with real or simulated inputs and check their outputs. The mathematical validity of each functional unit should be as good as that of the processes comprising it. It is advisable that you compare the outputs to expected mean and standard deviations of observed data, if they are available.

The performance checks you will run should reveal any significant problems concerning the internal processes or their interactions. You should correct them until you achieve a credible output. You should add any modifications you will make in the Processes Table. This will help you keep better track of your formulations and will also assist the documentation process.

Ballpark Simulation Model
At this point, it will be useful to further link up the functional units and the Input functions in order to make a working simulation model. Here are some reasonably good purposes for doing that:
• you will have the opportunity to check the plausible results before moving on the refined model.
• you will be able to reveal problems into the feedback loops between the different functional units.
• you will be provided with a working reference in order to justify any further modifications. This way you will retain and replace your ballpark model with upgraded versions during the refinement procedure, with the last version to be used always as a reference for making changes and debugging problems.

Refined Process Models
The results from the development, critique, testing, and grouping of the ballpark functional units models should provide you with guidance for how and what to upgrade in order to achieve better performance for the internal processes. You have to identify those approximations you made and that are the most probable suspects to decrease the accuracy or functionality of the process. For your own facilitation, after every change, you should check the refined version against the ballpark version.

Validation
At this stage you must check again the mathematical correctness of the process formulations. It is possible that the refined versions of the process models will not resemble the ballpark versions (e.g. more input variables and constants) and therefore you will need a more thorough review. In compensation, it is more than sure that you will find more literature references for the refined version than for the ballpark models.

Calibration
Calibration involves ajusting model parameter values until the model results correspon as well as possible to some observations. The data that you will need for the calibration processes do not necessarily need to be long time series. Often short time series including some characteristic events are the best for calibration. The challenging difficulty will be to find coincident, observational data for both the process inputs and outputs. If any coincident data is not available, you can use statistical correlations for a rough calibration. If not at all suitable data are available for a single process, you can conduct its calibration by grouping it with (an) other process(es) and calibrating their output altogether, or you can postpone it for later when it will be included in a functional component model for which there is calibration data available. For your own facilitation and for a better result, if the data are available, it is better to calibrate every process and then also run a calibration in the level of functional components.

Choke Points:
This is a term that expresses points in the system that are sensitive to many processes and therefore observations at these points of connection can be indicators of a combination of many processes and therefore of values for calibration. The simulated outputs of a complex system are not necessarily unique, as different combinations of multiple errors can sometimes produce the right answer. Ideally, it is best to make comparisons between observational data and modelled data at these choke points. However, only rarely are observations actually made at such choke points in the system. In practice, one has to use tricks with what is available.

Auxiliary Models
These are calculations or models formulated and tested outside of the selected software environment, but which are to be utilized within the simulation analysis, either in the simulation model or the interpretive analysis. For the one which will be integrated into the simulation model, there are several considerations concerning their coupling. More specifically:

• The results of the auxiliary models are not dependent on variables inside the rest of the Virtual System and have been computed during the same time interval and time step as the one used in the simulation model.
• The results may be added into the model as input data.
• The results of the auxiliary models have the same time interval and are independent of internal variables but they need some adaptation before insertion in the simulation model. The case may be that:
• the auxiliary model runs at another time step. Then the results require interpolation or averaging before you can add it to the model as input data.
• the auxiliary model calculates result in a finer spatial grid. Then the results require a real averaging before you can add it to the model as input data.
• the auxiliary model calculated by a mixture of methods to form defendable estimates – adapt to a data input, conversion table, or input function.
• The results of the auxiliary models have the same time interval but are dependent of internal variables inside the rest of the Virtual System. This category requires some form of parallel calculation. Advanced modelling skills are required in order to carry out the interconnection between the two models.

Assemble and test the simulation sub-models

ESE linkages
At this stage you should formulate the linkages between the ESE components. By linkages, we mean the points were the sub-models are connected to each other, i.e. an output variable from the one component is an input variable to the other component. This coupling between two models must have a dimensional agreement. In some applications, you may need to reformate the output in order to make the quantity compatible for the receiving model. In some other cases, you will need to use more complicated processes to convert the output of a component to a suitable input for the receiving component. You must formulate these interactions as a part of one of the implicated. These interactions must be absorbed into one of the Components involved. The Economic Component must specify what information it needs from the Ecological Component and in what format (indicators or variables, etc.). If a conversion is to be done in the Economical Component, it should be formulated. The plan for assessment should be drafted in order that any missing preparations can be fulfilled before the WT4.3. Similarly the scope of the SC analysis needs a reality check in terms of relevance to the other two Components, e.g. that it is analyzing a social response that is relevant to the results of the NC and EC. The preparedness to continue with the planned assessments should be assessed. An assessment plan should be drafted in order that any missing information or resources can be identified.

Examples: •The Ecological Component calculates the weight of the fish population and the Economical Component receives live weight of the fish supplied to the market. The conversion might require a harvest process (taking a portion of the live fish population) and a distribution process (to calculate loss in the procession to several markets). •The Ecological Components calculates the light absorption in the coastal water and the Social Components needs the perceived water quality of the bathing beach, which might be a function of the color, odor, wave conditions, or other properties of the water. The conversion would require some agreed indicator of bathing quality, e.g. a simple indicator of acceptable thresholds for wave conditions and turbidity.

Refined functional unit models
Here it is important to first review the performance and scope of the ballpark functional units models and then compare it to the refined functional unit models. Considerable scientific insight is needed to best portray these components.

A recommended sequence might be:

Review.
Make obvious changes in terms of the composition and structure of the refined version. More specifically:

• usually the refined process models need more inputs than the ballpark process models.
• in a functional component another process may need to be added.
• it is rather probable that more information input is needed.
• you may need to add an extra feedback loop to a functional component.

Restructure.
The refined version will most likely require more or different components. More specifically:

• if your application requires more than one herbivores, you may decide that is useful to develop a separate grazing functional component.

• the literature may provide many different structures for a functional component, like primary producers, but the modeller of your team must be careful to simplify and adapt for the requirement to your specific Virtual System and your simulation objectives.

• in order to satisfy some aspects of a management scenario you may need to include to your formulation both the economic assessment of an illegal and commercial harvest component.

Replace Processes.
You should replace the refined process models one at a time in order to keep track of any destabilization changes or abnormal behavior of the model.

Validation & Calibration
All the functional units that you have developed should be validated and calibrated separately before you attempt to validate and calibrate the ESE components. You must note all the approximations that you will make to the formulas you will use or that you will do during the process of testing the model. You should also make a discussion from the point of view of sensitivity and potential error, as it will later facilitate you with the documentation of your analysis. You model should be validated over the range of conditions that are usually expected with application in your Virtual System. That is translated into a validation concerning the maximum and minimum values of the input variables and into a validation concerning any external non-linear feedback loops that should be also tested over the expected ranges of the external component. You should also calibrate your models with the best data available. In case that these data do not present the complete range of variability as you would like for use in the simulation model it is necessary that you should contact additional sensitivity tests ensure that the outputs are within the broader range of observations. Note that it is not necessary to use calibration data the same time-period for all the functional components of the model.

Refined ESE Models
In a previous subtask, there was a description of how you will develop the ESE ballpark models. The intervening subtasks have helped clarify the scope and need for improvement in the ESE component formulation. For the refinement procedure for each might be:

Review.
The ballpark models you will develop are probably using a number of approximations, but nevertheless they should operate within the range of variability observed in your Virtual System. This is why they can be useful reference models. However, they are inadequate in terms of portraying change in complex systems, because the internal interactions are under-represented. In addition, they were not constructed to satisfy all of the scenarios or to accommodate certain of the potential risks. The reason for reiterating this is to make sure that a careful review is made of what is expected from each of the ESE models in light of the simulation analysis. During the Appraisal Step, you must minimize as possible the need for any further model restructuring.

Restructuring.
By the term restructure we mean the replacement of the components of the ballpark ESE models with their respective refined functional components. Either modellers tend to do this by rebuilding the refined version without much referral to the ballpark version, or they rebuild the ballpark version component by component by component by component with constant referral to previous versions. The latter is recommended especially for less experienced modellers.

This approach involves replacing components, or processes, one at a time and running the model to make sure the results are still in the proper range. After each replacement, the model is saved with another version number. This approach has the advantages of better understanding the role of each component/process and of minimizing the need for extensive debugging. However, it can have the disadvantage of needing some format reorganization at the end of its construction.

Test ESE Models
If you have developed different models for each of the ESE components you need to test them independently before proceed to the Appraisal Step. After these tests, they will be calibrated with hindcast data.

Validation.
Most of the components will have been previously validated, but the ensemble of connected components (and new components) must also be thoroughly checked for mathematical and other mistakes (units, connections, initial values, calculation order, etc.)

Sensitivity Tests.
The same could be said about sensitivity checks, except that the refined model will have more complicated interactions that will affect its sensitivity to changes in certain of its parameters or inputs.

Range of Validity.
If you will the “replacing” approach to construct the model you can check the output variables as they are replaced. Thus, you can easily identify the problem if the model’s output goes out-of-range or it blocks the simulation. When you connect components, it is sometimes useful to insert a constant for a variable to facilitate you identify any out-of-range problems.

Linkages.
The linkages were defined in a previous subtask, but they need another review when the actual ESE Models are in their final form. Discrepancies are dealt with by either changing the model or by changing the scenario requirements.

Hindcast models
You may often find yourself answering ‘what if’ scenarios that are characterized by calculating results under hypothetical conditions. The same as predicting climate change such hypothetical results are rendered more credible if the model can successfully predict ‘past’ results e.g., to predict aspects of this years’ climate by starting the model many decades ago. This type of model calibration is referred to as ‘hindcasting’.

The credibility of your simulation models is necessary in order to develop a functional science-policy interface. The simulation models developed through the implementation of the SAF, as with the climate-change analogy, are used to forecast conditions in the future, although over much shorter time scales. Since the dynamics of Ecological systems are more deterministic and the socio-economic systems more behavioural, forecasting of complex coastal zone systems will be subjected to scepticism.

In many cases, it will be difficult to find sufficient data to conduct hindcast runs. In the end of the Formulation Step you should have the calibrated ESE models in order to proceed to the Appraisal Step, which conducts tests on the Simulation model (combined ESE model). Because of the anticipated difficulty to find hindcast data, it is best to conduct separate hindcasting experiments with each of the ESE Component models.

Some examples would be: Ecological Component : Five years ago a new treatment plant was installed which reduced the total nitrogen loading of an estuary by 20%. Does a simulation starting 6 years ago, and which matches the initial conditions, show agreement with present conditions? Economic Component: A hurricane devastated the aquaculture output 5 years ago, does a simulation run of this event reflect the present level of employment in this aquaculture? Social Component: A doubling of tourism occurred between 5-7 years ago, does the simulation of this period reflect the current change in tourism infrastructure.

The ESE components models should be modified as necessary according to the results of the hindcast runs. The ESE Hindcast Models will be used at the beginning of the Appraisal Step for aspects of the interpretive analyses of each ESE Component in the form of independent assessment tools. This subtask serves for the final check of the products and information past onto the Appraisal Step.

Next step